Nadal de 1610. Un home cruza o Puente de Carlos en Praga, neva e as folerpas caen sobre a lapela do seu abrigo. É Johannes Kepler, pensando en que agasallo de Ano Novo podería ser o máis apropiado para o seu benefactor e amigo Johannes Matthäus Wäckher von Wackenfelds.
Observa as folerpas de neve, e nelas atopa unha estraña regularidade. Como bo científico, non pode evitar preguntarse por que todas teñen forma hexagonal, e non cinco lados, ou sete?

Kepler pensa que este tema podería ser o motivo para un ensaio, un excelente agasallo de Ano Novo para o seu benefactor. Así escribe a súa obra Strena seu de nive sexángula (A folerpa de neve de seis ángulos), un libriño dunhas escasas 24 páxinas que constitúe, sen dúbida, unha obra mestra.
Na introdución Kepler escribe ao seu amigo:
Si, sei ben o afeccionado que é vostede á nada; de seguro non tanto polo seu mínimo valor, senón polo xogo divertido e delicioso que un pode ter con ela, como se fose un pardal feliz. Por tanto, imaxínome que para vostede un agasallo debe ser mellor, e mellor recibido, canto máis se achegue á nada
Kepler ironiza aquí coa súa situación en Praga, sempre pendente dos pagos a destempo e recortados de Rodolfo II, en cuxa corte traballaba Kepler de astrónomo, porque que mellor regalo que dar nada para quen nada recibe? Por outra banda, Kepler fai un xogo de palabras con nix (latín) que significa neve, e nichts (alemán), que significa ‘nada’. Kepler pensa ademais que non haberá mellor agasallo nesas datas que reflexionar sobre algo que cae do ceo.
Por que a forma hexagonal das folerpas?
No ambiente de tranquilidade da cidade é cando Kepler escribe Strena seu de nive sexángula. A análise de Kepler é profunda, e deduce que a forma particular das folerpas de neve debe ser consecuencia da maneira na que se empaquetan as partículas que as constitúen. Kepler unifica así dous conceptos: o mundo xeometricamente ordenado e creado por un Deus matemático cunha ciencia que trata de explicar os fenómenos naturais buscando as causas e leis que os producen.
Pódese pensar nesas partículas como glóbulos que se amontoan ocupando o mínimo espazo posible, e o ‘empaquetado’ hexagonal é o mellor. Basta ver as colmeas das abellas, ou as teselacións dun plano, que poden ser de triángulos, cadrados ou hexágonos.
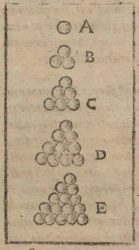
Neste mesmo ensaio, Kepler expuxo a súa famosa conxectura de empaquetado, resolta 300 anos despues por Thomas Hales. Anos antes, Kepler compartira correspondencia co astrónomo e matemático inglés Thomas Harriot, acerca da maneira óptima de amontoar balas de canón na cuberta dun buque. Sir Walter Raleigh, de quen Harriot foi axudante, expuxéralle a cuestión cando estaban a planificar unha expedición en 1585 rumbo a Virxinia, a fin de establecer alí a primeira colonia británica.
A conxectura de Kepler establece que a mellor maneira é a que usan nas froiterías para as laranxas, poñendo cada laranxa da seguinte capa apoiada no oco das catro laranxas que están xusto debaixo na primeira capa. Este método minimiza o espazo deixado polos ocos entre as laranxas.
Durante séculos, trataron de demostrala numerosos matemáticos como Gauss, que a probou no caso regular. No Congreso Internacional de Matemáticos de 1900, foi incluída por David Hilbert na súa lista dos 23 problemas máis importantes para o século XX (o problema número 18). Pero o asunto non tivo maiores avances ata que o matemático húngaro Laszlo Fejes Toth reduciu o problema a un número finito pero enorme de cálculos. Thomas Hales foi capaz de realizar as contas nos anos 90, axudado pola potencia do computador. O resultado publicouse en Annals of Mathematics (PDF), e con iso a conxectura quedou resolta. Aínda que hoxe en día non todos os matemáticos aceptaron que isto poida considerarse unha auténtica proba.
O que hoxe sabemos da neve
Kepler non tiña o coñecemento actual de como está constituída a materia. Non sabía que unha molécula de auga está formada por dous átomos de hidróxeno e un de osíxeno, formando un ángulo de 104,5º. Estas moléculas de auga están ligadas con enlaces coas súas veciñas, formando tetraedros. Cando a temperatura baixa, achéganse máis entre si e forman esas estruturas de seis lados.
Se esta explicación non resulta satisfactoria, e queremos unha máis poética, pódese recorrer á lectura do precioso relato The Queen of the Rain Was in Love with the Prince of the Sky, escrito por Eugene Mirabelli; que tamén mostra por que dous flocos de neve nunca son iguais.
* Manuel de León é profesor de investigación do CSIC no Instituto de Ciencias Matemáticas (ICMAT-CSIC). Unha versión deste artigo foi publicada orixinalmente en en o blogue Matemáticas e as súas fronteiras, da Fundación para o Coñecemento madrid+d.
Cláusula de divulgación: a autora non recibe salario, nin exerce labores de consultoría, nin posúe accións, nin recibe financiamento de ningunha compañía ou organización que poida obter beneficio deste artigo, e declara carecer de vínculos relevantes alén do cargo académico citado.














