A sección de meteoroloxía ocupa unha parte destacada nos telexornais de todas as cadeas. Esta sección, á parte de informarnos da situación do tempo de cada xornada, axudounos a comprender conceptos como a probabilidade de choiva ou a imposibilidade de saber un luns se o domingo poderemos ir á praia.
No caso das epidemias, outro fenómeno moi difícil de explicar, a incerteza de cando chegará (ou chegou) o cumio e canta xente vai ingresar no hospital a semana que vén convida a usar unha variedade de modelos matemáticos chamados cadeas de Márkov.
No noso obxectivo de achegar á sociedade os instrumentos matemáticos que nos axudan a enfrontar a actual pandemia, facémonos eco da figura dun matemático excepcional, Andréi Andréyevich Márkov, o inventor das cadeas que levan o seu nome.
Estudos e inicios na probabilidade
Márkov naceu en Riazán, Rusia, o 14 de xuño de 1856. O seu pai, fillo dun diácono rural, estudou nun seminario, conseguindo posteriormente un emprego no Departamento Forestal en San Petersburgo. Andréi era o maior dos dous fillos homes nunha familia numerosa. O seu irmán menor, Vladimir, morto prematuramente de tuberculose, conseguira na súa curta vida unha gran reputación como bo matemático. O primoxénito era un neno cunha saúde delicada que levou muletas ata os dez anos pero, xa na secundaria destacou en Matemáticas, chamando a atención dos seus profesores.
Era obvio que Márkov ía estudar esta materia, e así o fixo na prestixiosa facultade de Física e Matemáticas da Universidade de San Petersburgo. Alí recibiu unha forte influencia do brillante matemático Pafnuty Lvovich Chebyshev (Okátovo 1821 – San Petersburgo 1894).
Márkov graduouse en 1878 e comezou o seu traballo de máster sobre teoría de números (aproximación racional), unha tese que foi moi encomiada e considerada un dos mellores tratados sobre o tema nesa época. Isto permitiulle seguir a súa carreira como profesor da universidade e conseguir o doutoramento en 1884. Dous anos despois, converteuse en adxunto da Academia de Ciencias de San Petersburgo a proposta de Chebyshev, aínda que seguiu mantendo a súa vinculación coa universidade.
Foi en 1900 cando Márkov comezou a interesarse pola teoría de probabilidade, tema no que obtivo resultados moi brillantes, incluído o descubrimento das cadeas que levan o seu nome.
Chebyshev, Kolmogorov e Márkov son os grandes nomes que usaron elementos da teoría da medida para converter a teoría de probabilidade nunha das áreas máis rigorosas e respectadas das matemáticas.
Márkov non traballou pensando nas posibles aplicacións prácticas das cadeas que descubriu. De feito, a única área onde as empregou foi na literatura, contando vocais e consonantes, quizais polo seu gran amor á poesía. Con todo, como amosamos a continuación, as aplicacións das cadeas de Márkov son de gran utilidade práctica.
As cadeas de Márkov
De maneira intuitiva, unha cadea de Márkov en tempo discreto (por sinxeleza) é un proceso estocástico que evoluciona en tempo discreto ou etapas, e ten a propiedade markoviana que di: “o futuro depende do que pasa no presente, pero non do pasado estrito”.
Así, teremos uns estados E₁, E₂, E₃,… de xeito que se pasa dun a outro por unha matriz de transición nunha etapa. A cardinalidade (número de elementos) do conxunto de estados é numerable, é dicir, é un conxunto finito ou coa mesma cardinalidade que os números naturais.
A matriz de transición en cada etapa ten como elementos ás probabilidades de paso dun estado a outro cando o proceso evoluciona desde unha etapa ‘n’ á etapa seguinte ‘n+1’. Por tanto, está composta de números reais positivos entre 0 e 1, de maneira que a suma de cada fila ou columna, segundo a disposición dos estados inicial (na etapa ‘n’) e final (na etapa ‘n+1’), é 1.
Aplicación en medicina
O seguinte é un exemplo moi sinxelo. Nunha unidade de coidados intensivos, os pacientes clasifícanse (triaxe) atendendo ao seu estado: crítico, serio e estable. Cada día actualízanse as clasificacións de acordo coa evolución histórica dos pacientes admitidos na unidade ata ese momento, de modo que as frecuencias relativas de cambios de estado dun paciente son:
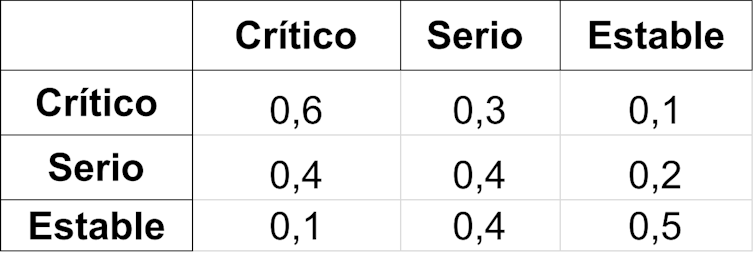
Na disposición anterior, as entradas por filas están asociadas ao estado do paciente no día ‘n’ e as columnas refírense ao seu estado no día ‘n+1’. Entón, poderiamos tomar como matriz de transición nunha etapa:
As filas suman 1. Unha representación gráfica como a seguinte pode axudarnos a entender mellor a dinámica de cambio entre estados dun paciente en dous días consecutivos:
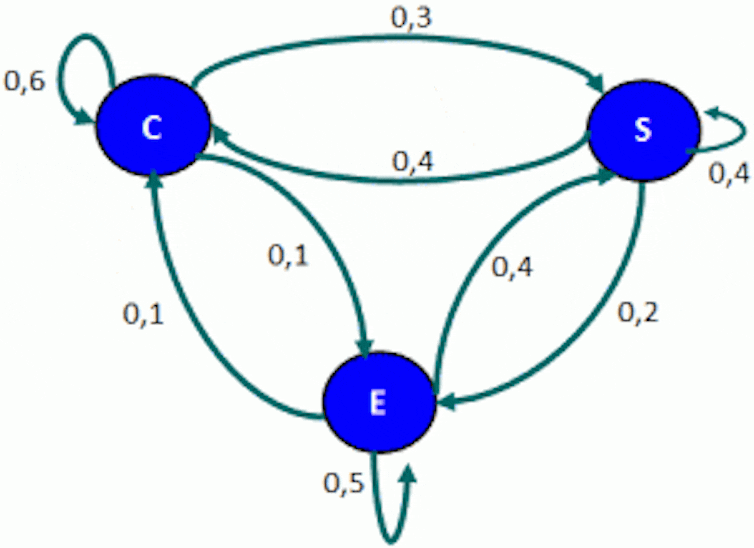
Cun gráfico como este podemos calcular probabilidades en máis dunha etapa. Por exemplo, a probabilidade de pasar do estado crítico C a estable E en dous días. Hai tres posibles camiños, dependendo do estado C, S e E do paciente despois do primeiro día:
C –> C –> E
C –> S –> E
C –> E –> E
Só temos que multiplicar as probabilidades e sumar da forma:
0,6 × 0,1 + 0,3 × 0,2 + 0,1 × 0,5 = 0,17
É dicir, un paciente ingresado en estado crítico C evolucionará ao estado estable E en dous días nun 17% das ocasións. Evidentemente, estas probabilidades poden cambiar conforme aparecen novos tratamentos, ou poderían definirse distintos estados da cadea atendendo á idade do paciente, etc. Todas estas xeneralizacións enriquecerían a cadea de Márkov, pero a idea xeral seguiría sendo a mesma.
Compromiso político e social
Márkov era unha persoa comprometida politicamente nunha época, principios do século XX, de transición axitada de Rusia. Por exemplo, cando a Maksim Gorky se lle retirou o seu nomeamento como académico da Academia de Ciencias por razóns políticas, protestou enerxicamente.
En 1913, o matemático negouse a secundar a celebración do terceiro centenario do zarismo para celebrar, pola súa conta, o segundo aniversario da Lei dos Grandes Números.
Cando triunfou a Revolución Rusa de 1917, Márkov solicitou que o enviasen a un pequeno pobo do interior, Zaraisk, a ensinar na escola local de maneira gratuíta e así contribuír á mellora da pobre sociedade rural.

Afectado de graves problemas de saúde, este brillante matemático ruso faleceu en San Petersburgo o 20 de xullo de 1922. Morreu aos 66 anos de idade debido á infección xeneralizada producida por unha das varias operacións cirúrxicas de xeonllo ás que foi sometido.
* Manuel de León é profesor de investigación do CSIC no Instituto de Ciencias Matemáticas (ICMAT) e membro da Real Academia de Ciencias; Antonio Gómez Corral é profesor do Departamento de Estatística e Investigación Operativa da Universidade Complutense de Madrid; Mario Castro Ponce é profesor e investigador na Escola Técnica Superior de Enxeñaría (ICAI) da Universidad Pontificia Comillas.
Cláusula de divulgación: Manuel de León non recibe salario, nin exerce labores de consultoría, nin posúe accións, nin recibe financiamento de ningunha compañía ou organización que poida obter beneficio deste artigo, e declarou carecer de vínculos relevantes alén do cargo académico citado; Antonio Gómez Corral recibe fondos do Ministerio de Ciencia e Innovación; Mario Castro recibe fondos do Ministerio de Ciencia e Innovación e a Unión Europea a través do programa H2020.